Clustering and Gene Ontology
Contributed by Laura Mulvey and Julian Gingold
Introduction:
Why do we need clustering? Differential expression allows researchers to look at a specific gene's behavior over a set of samples. However, differential expression only allows us to look at a single gene at a time. There exists a need to look at more complex networks of genetic changes. For example, genetic changes could directly result in a shift to cancer, or a genetic change may be more indirectly linked. Clustering allows us to look at genetic changes that can be grouped together, it throws out the notion that all genetic changes are independent events.
Why do we need gene ontology? Once we have the gene clusters, we need to identify their functions: gene ontology systematically describes these known genes. With the appropriate statistics, we can then discover upregulated pathways/processes/cellular components, identify new members these groups and discover whether these groups are differentially expressed.
Clustering
Clustering analysis can be performed on genes or on samples. When two genes cluster together, they have a similar expression profile across all the samples, and when two samples cluster together, they have a similar expression profile across all the genes. There are dozens of different clustering algorithms in use, which can all yield different results. However, in general, clustering allows us to visualize data in the form of a heat map, better understand our data, determine rough genetic differences across samples, and sort our samples based upon their genetic profiles. A heat map from is shown below. In this experiment the authors were looking at the genetic changes that chimps infected with HCV undergo. This heat map is an example of 2-D clustering, as both the genes and samples are clustered simultaneously.

Clustering can be performed in either a supervised or unsupervised manner. In supervised clustering, the is a predetermined number of sets or classes, while in unsupervised clustering, there is no preset numbers of classes. K-means and self-organizing maps are examples of supervised clustering. Supervised clustering is used to classify objects into known classes. We will discuss later the prediction of cancer class and treatment options from a gene expression profile. Heirarchical clustering is an example of unsupervised clustering. There are many ways to ensure the stability of the cluster. We can mask out some data, by only sampling a subset of genes or samples to perform the clustering, introduce a little noise to the data, or filter only differentially expressed genes (for full description see previous chapter) for clustering, or use genes in the sample pathway.
Similarity Measures
Most clustering algorithms make use of a matrix of distances between data points. These distances form the basis of similarity/dissimilarity between what is being clustered. There are a variety of ways to calculate the distances. They include the Euclidean distance, Pearson correlation coefficient, and weighting.
Euclidean Distance
The Euclidean Distance is the straight line distance between two objects or clusters, taking into account direction and magnitude.

Pearson Correlation
The Pearson Correlation coefficient (rxy) varies from -1 to 1 and looks at whether two genes have a similar expression: if they vary in the same way. Genes that have similar expression profiles, even if they have different basal levels of expression will have a high pearson coefficient.

The distance is given by:

We can see through this formula that objects with a high Pearson coefficient will have a small distance between them.
Weighting
Sometimes, we want to weight different observations differently. When clustering genes, replicate experiments should have a smaller weight. When clustering experiments, genes in the same family should have smaller weight.
The weighted algorithm is given by the following equation:

KNN for Missing Value Estimation
As might be expected, missing values affect clustering such as for distance calculations. The naive solution to this problem is to ignore the gene or sample and fill in 0 or average. However there is a more statistically significant method for missing value estimation, called KNN (K nearest neighbors).
KNN was first described by Fix and Hodges in 1951. After measuring the Euclidean distance between all objects within a set, each object is assigned to a specific class. The objects' k-closest neighbors are found. The neighbors are then analyzed to see which class most belong to. That object is then assigned the class that correlates with the majority of its neighbors.
When applied to missing value estimation, say gene i has a missing value at sample j. We can calculate the correlation between gene i and all other genes using all samples except j. Then we find k genes with the highest correlation to i. We calculate k genes' average expression at sample j and assign that value to gene i.
Clustering Algorithms
Two Way Clustering
Two Way Clustering is when genes and samples are clustered independently and then combined.
Hierarchical Clustering and Linkage
Hierarchichal Clustering is when clusters result from a branching process. There are two ways to calculate hierarchical clustering: agglomerative nesting methods and divisive analysis methods. The differences are outlined in Smolkin et al. Agglomerative nesting is the most commonly used form. It takes a bottom up approach, repeatedly. Here the two most similar nodes are merged. The distance from the newly formed node to all other nodes is calculated. Then, the next two similar nodes are merged until 1 node remains. The branch length between different nodes is proportional to the relative difference between objects. The divisive analysis method is sort of the reverse of the agglomerative nest methods. All the objects are in one node. The most dissimilar object is splintered off, to create two nodes. This continues until there are as many nodes as objects.
The following figure shows hierarchical clustering of genes for four different samples.

Linkage, or the distance from a newly fourmed node to all other nodes, can computed in several different ways: single, complete, and average. The figure below roughly demonstrates what each linkage evaluates:

Single linkage defines the distance between clusters as the distance between the closest two points. The distance between two clusters cj and ck measured by single linkage is described by the formula below, where cu and cv are two clusters just merged into cj.

Single linkage can lead to a lot of singleton clusters, and to clusters that look stringlike in high dimensions.
Complete linkage defines the distance between clusters as the distance between the farthest two points. It is described by the following formula:

Complete linkage tends to lead to more compact spherical structures.
Average linkage is the average of all the pairwise distances between points in the two clusters. It is described by the formula below:

Average linkage is between single and complete linkage in terms of the type of clusters it outputs.
Partitional Clustering
Partitional Clustering differs from hierarchical vlustering in that it yields a number of disjoint clusters. The following figure shows the interrelationship between hierarchical and partitional clustering.

A partitional cluster can cut a hierarchical cluster and separate genes or samples into distinct groups. By varying the cut height, we can produce an arbitrary number of clusters.
K-means
K-means clustering is the best known partitional clustering technique. The K-means Algorithm requires that there is a predetermined number of K centroids. This is a crucial step because if too few centroids are chosen, disparate genes or samples will be gouped together. If too many centroids are chosen, similar genes and samples will not cluster together. The commonly accepted method for determining how many K to pick is to start with K=2 and gradually increasing. A productive increase in K will reduce the distance within clusters, and increase the distance between clusters. However each increase in K separate genes that are similarly expressed. There are several ways to calculate when an appropriate K has been reached. According to Calinski and Harabasz (1974), the maximum K should be:

where W(k) is the total sum of squraes within culsters, B(k) is the sum of squares between cluster means, and n is the total number of data points. In 1975, Hartigan offered a different test for max K:

The user should stop increasing K when H(k)<10.
After choosing K centroids at random, an object i is assigned to its closest centroid. The centroid's position is then recalculated based upon the current cluster assignment. These recalculations are repeated until the assignments stabilize. Then the clusters split, and the centroids are recalculated until the number of centroids is K and all the assignments are stabilized.
The following figure shows K-means clustering of normalized microarray gene expression data with K=20.

There are several caveats to the K-means algorithm. It is a deterministic method, meaning the initial cluster ceters are important, as a centroid can be trapped in a local optimal. Therefore, the initial cluster centers are usually picked after hierarchical clustering is conducted on the samples, and the cut lines are determined (similar to previous figure). Also, there can be many random starts with different initial centers. Lastly, the K-means Algorithm is not tolerant to noise or outliers. The algorithm forces every data point to a cluster. Therefore, outliers tend to pull the cluster centers away from their ideal position.
PAM or Partition Around Medoids is an attempt to remove some of the drawbacks of the K-means algorithm. It involves picking one real data point that is closest to all as the centroid position, rather than averaging the positions of all data points within the cluster. This makes it more robust in the presence of noise and outliers.
Tight Clustering was described by Tseng and Wong in 2003. A random sample X' which represents about 70% of the original data was chosen to perform K-means clustering. The clustered centers were then utilized to classify the original data and fill the co-membership matrix. In tight clustering, sampling is repeated many times and average co-membership calculated. Sets with high average co-membership are identified. This method produces tight and stable clusters. It is noise tolerant and obtains biologically relevant genes. The innovation of this method is that it does not force clustering of all data points. It ignores genes that don't fit in any cluster.
Self-organizing maps
SOM, or self-orgnaizing maps is yet another clustering technique. It was created to model neural networks, but has been applied to the analysis of microarray expression data. An n x m grid is randomly chosen an the analysis is initialized. A gene l in sample x is randomly picked. Each node is moved toward x, with the closer ones moving more. It is an iterative process, so after every random pick, the move step is decreased.
The figure below is a SOM data set from a microarray experiment You may notice that clusters close to each other on the SOM have similar expression profiles.

Applications: The Swedish Breast Cancer Project
Clustering has been widely used to analyze microarray data, and results from these experiments have proven valuable. There is one such example of an effective application of clustering and microarray techniques to the field of breast cancer diagnosis and treatment. In 2001, a Swedish group headed by van't veer published a study in Nature entitled, "Gene expression profiling predicts clinical outcome of breast cancer." The authors ran a two-dimensional hierarchical clustering analysis on 98 breast tumors for 5000 genes they deemed significant by differential gene expression. They then looked how the breast tumors clustered. Given that they were all different subtypes of tumors. They looked at the presence of BRCA-1 mutations, ER expression, tumor grade, lymphocytic infiltration, angioinvasion, and metastasis status. Their clustering methods were able to distinguish among samples with different lymphocytic infiltrations, and ER status. The authors then decided to focus on the 78 tumors without lymphocytic infiltration. They tracked the prognosis of these patients, with the hope of being able to point to specific gene clustering patterns that would differentiate between the various prognoses. Of the 5000 genes in the initial screen, 231 of these significantly correlated with disease outcome. They eventually whittled down this list to 78 genes. The figure below shows the correlation between the expression of these genes and disease prognosis.

The authors then established a signature that sorts tumors on the basis of BRCA-1 mutations. They close the paper with the statement, "This gene expression pattern will outperform all currently used clinical parameters in predicting disease outcome." Because of microarray technology, and clustering techniques, the investigators were able to design several "disease" and "prognosis" signatures. The ease of BRCA1 mutation detection has an impact on preventing breast cancer, and the prognosis signatures identify patients that are in need of more rigorous therapies. A recent study by Paitwan et al. using the same methods identified breast cancer patients that would not benefit from adjuvant therapy. These studies have the power to bring microarrays to the clinical setting, and alter the quality of life, and health of cancer patients.
Gene Ontology
Gene Ontology provides a thorough annotation of the genes and pathways used in a biological system. The wide variations in terminology that currently abound in biology can often hamper the prospect of finding relevant results. A consistent nomenclature allows "protein synthesis" and "translation" spares the user from searching for synonyms.
The Gene Ontology Consortium began in 1998 with the aim of annotating all gene functions in 3 model organisms--mouse, fly and yeast. Since then it has been extended to include data from multiple organisms.
This is particularly useful when you are studying a gene in one organism whose complete function is unknown. Based on the gene ontology data from its ortholog in another organism in the database, one can infer its interaction partners, functions and pathways.
The structured database facilitates search at all different levels of specificity in biology, from a general protein catalytic function to an annotation of each protein.
Below is a the gene ontology and structure from eukaryotic translation elongation factor 1 (Source: AmiGO Gene Ontology Database)

Annotations in the Gene Ontology database
All terms in the GO database are organized by a numerial identifier, GO:nnnnnnn and a term name, e.g. signal transduction.
These terms are fit into 3 ontologies:
- Molecular Function Describes the catalytic and chemical functions of a protein. Binding is a molecular function.
- Biological Process Allows one to specify into which pathways this protein fits and when it is activated. Can also describe a state in the cell cycle. Molecular transport is a biological process.
- Cellular Component Describes cellular localization to identify where in the cell this protein is found. Ribosome is a cellular component.
Structure of GO
The database is a tree-based hierarchy defining two types of relationships: is_a and part_of
- is_a (abbreviated as i) means that the child "is a kind of" the parent. Cell differention is a kind of cellular process
- part_of (abbreviated as p) means that the child "consistitutes one part of" the parent. Cell fate commitment and cell development are both parts of cell differentiation.
Formally this is called a directed acyclic graph, because one can only move down in the hierarchy (no subsection can have a subsection that is its own parent) and because the same term can appear in multiple branches (i.e. a growth factor can also be grouped with other phosphotransferases that do not have to do with growth).
Limitations of GO
GO's current structure limits ontology information to the scale between proteins and cells and only describes the normal, functional cellular components as they are. It lacks details on gene products, diseases/mutations, various gene splicings, protein-protein interactions, protein domains, gross anatomy, environment, evolution and expression.
One application of Gene Ontology is in identifying pathways and proteins associated with cancer. By comparing the gene expression profiles of normal, precancer, and cancer cells, one can develop a better understanding of the science underlying cancer and ultimately lead to improved treatment. This tool was designed to allow one to identify orthologous genes between humans and mice based on GO terms and draw human connections from mouse models.
Below is an example of a high-level Gene Ontology for biological processes involved in cancer from CGAP.

Evaluating the Significance of Differential Expression
The main purpose is to be able to decide whether we are seeing a statistically significant up/down-regulation of a specific gene. What is the random chance that a certain set of genes will be mapped to a set of GO terms. If 80 of the 100 genes in a GO term are upregulated in an experiment and there are 20k genes assayed, how do we quantify the significance this observation?
Binomial proportion test
The binomial test compares dichotomous data in which a sample falls into two categories, e.g. being upregulated or not, and tests whether this categorization differs from the expected grouping. In this case, we want to test whether the upregulated genes are associated with a particular GO term more than the genes in the whole genome have this term. This test is technically only significant if both n*p>10 and n(p-1)>10. While this example is not appropriate for the statistics, we will do the sample calculation anyway. Following the formula below, one calculates z and checks the results in z table. x is the number of upregulated genes with GO term X, n is the number of upregulated genes and p is the percentage of genes in the whole genome that have GO term X (in our case, 100/20,000). Larger values of z are more significant.

For more information, see this page.
Chi Square test
Organize the categorized data in a table. The observed values are listed first, and the calculated expected values are in parentheses:
| Up | !Up | Total |
| Go: | 80(1) | 20(99) | 100 |
| !Go: | 120(199) | 20k-220(19701) | 20k-100 |
| Total: | 200 | 20k-200 | 20k |
In this example, the number of GO terms we expect not to be upregulated is (total !Up) times (total GO) over total genes = (20k-200)*100/20k=99
Calculate sum of the square of differences between expected and observed and divide by the expected to get a value that can be looked up in a chi-square table.
This is described mathematically as:

A higher number indicates greater significance. Our example has a chi-square score of:  , which is extremely significant.
, which is extremely significant.
Using GO to improve clustering
After calculating a cluster, look up its GO terms and see if there are any enriched terms. Are there any cluster members that do not "belong?"
For an unknown gene that fits into a cluster, see if it can be grouped with the GO term of the other genes in its cluster. This can allow one to infer the gene's function by being, in a sense, guilty by association.
Gene Enrichment Analysis
It might be possible that in a microarray experiment no single gene is significcantly differentially expressed. However, a group of genes might be slightly differentially expressed. If these collectively differentially expressed terms are similarly annotated (e.g. by a GO term), how can we assign a number to determine the statistical significance of this difference?
Kolmogorov-Smirnov Test
Determines how significant are two datasets while making no assumptions about the distribution of data. The cost of this generality is a loss of sensitivity. This test is useful when the T-test is not valid, either because the mean in two datasets is the same or because there is a non-normal distribution of data and a small number of points in the sets.
In order to note differences, we make a plot of the cumulative fraction function (also known as the empirical distribution function). The cumulative fraction at x is the fraction of the data strictly smaller than x. Thus if 17 of 20 points are strictly smaller than 3, then the cumulative fraction at 3 is 0.85. One graphs the cumulative fraction function of both datasets, e.g. a group of genes clustered according to some GO term and the set of all genes in the genome. It might be appropriate to use a log scale for x; the cumulative fraction function is by construction between 0 and 1 and monotonically increasing. This plot is shown below for two hypothetical data sets comparing one group to a control:
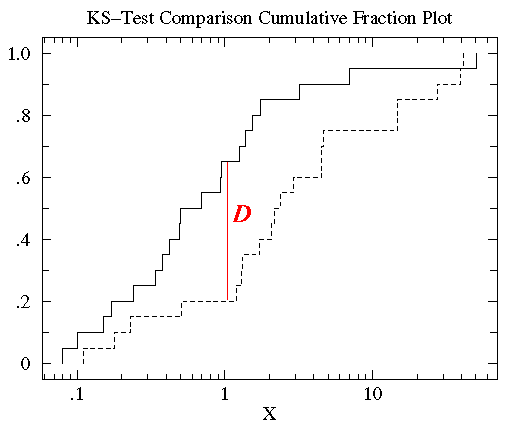

Considering the left case, if the dashed line is the group of genes in GO, and the solid line is the control of all genes, it is clear that even though these values have about the same range, by and large the GO set has lower values (levels of gene expression) than the control. The statistic on these data is called D, and is the maximum vertical distance between the two plots. Here D=0.45, since 65% of the data in the control is greater than 1, whereas only 20% of the data in the subgroup of genes is greater than 1. This log-distributed data does not get skewed by a Kolmogorov-Smirnov test. Similarly, the right plot shows how to distinguish between data with a similar median but different variation.
One-Sample Z-Test
Even if the plot of two gene sets looks the same, a certain subset of these genes with a particular GO annotation might actually be differentially expressed.
Assuming that the complete population of genes in the genome follows a normal distribution N(µ,σ^2) (with mean µ and variance σ^2), one can calculate the z-value of a particular subset of genes, X. z is then the difference between the mean of the subset X and the overall mean µ divided by the standard deviation σ times the square root of the number of annotated genes in set X. This is mathematically described as:

The null hypothesis would yield z=0, and thus the greater the absolute value of z, the more significantly different is the gene set from the entire genome.
Conclusions:
Clustering is a powerful and effective way to analyze microarray data. It recognizes that within the cell there are complex interactions involved in gene expression and regulation. Clustering allows us to identify which genes act similarly in different conditions. The use of clustering to look at disease signatures and prognosis is burgeoning within the medical genetics community, and will most likely lead to the use of microarrays as a clinical diagnostic tool.
Gene Ontology allows us to categorize genes according to function, location or pathway with a hierarchical structure consistent among different organisms. Once a microarray experiment identifies differentially regulated genes, one can use the binomial proportion test or the chi-square test to assess whether these genes correspond to any particular GO term. New functions of genes can be inferred in a microarray experiment if these genes cluster with known GO terms. A slightly differentially expressed group of genes (perhaps annotated by GO) can be identified with the Kolmogorov-Smirnov test or the one-sample z-test.
References:
- Online lecture notes and textbooks in this area.
How to Cluster Microarray Data (pdf)
An Introduction to Gene Ontology
Binomial Distribution: Binomial and Sign Tests
Wikipedia Chi Square Test
Kolmogorov-Smirnov Test
- Papers
- Cho RJ, Campbell MJ, Winzeler EA, Steinmetz L, Conway A, Wodicka L, Wolfsberg TG, Gabrielian AE, Landsman D, Lockhart DJ, Davis RW. 1998. A genome-wide transcriptional analysis of the mitotic cell cycle. Mol Cell 2(1):65-73. Abstract
- Pawitan, Y., Bjohle, J., Amer, L., Borg, A.L., Egyhazi, S., Hall, P., Han, X., Holmberg, L., Huang, F., Klaar, S., Liu, E.T., Miller, L., Nordgren, H., Ploner, A., Sandelin, K., Shaw, P.M., Smeds, J., Skoog, L., Wedrenm, S., Bergh, J. 2005. Gene expression profiling spares early breast cancer patients from adjuvant therapy: derived and validated in two population-based cohorts. Breast Cancer Res. 7(6):R953-64. Abstract
- Smolkin, M., and Ghosh, D. 2003. Cluster stability scores for microarray data in cancer studies. BMC Bioinformatics. 4:1-7. Full text
- van 't Veer LJ, Dai H, van de Vijver MJ, He YD, Hart AA, Mao M, Peterse HL, van der Kooy K, Marton MJ, Witteveen AT, Schreiber GJ, Kerkhoven RM, Roberts C, Linsley PS, Bernards R, Friend SH. 2001. Gene expression profiling predicts clinical outcome of breast cancer. Nature. 415:530-536
Abstract
Comments (0)
You don't have permission to comment on this page.